데이터 엔지니어
백준 - [Gold 5] 1916번 최소 비용 구하기 본문
문제링크: https://www.acmicpc.net/problem/1916
1916번: 최소비용 구하기
첫째 줄에 도시의 개수 N(1 ≤ N ≤ 1,000)이 주어지고 둘째 줄에는 버스의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 M+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그
www.acmicpc.net
문제 설명
- N: 도시의 개수
- M: 버스의 개수
- (출발 도시, 도착 도시, 버스 비용) M개
- 시작도시, 끝도시
위와 같은 입력이 주어졌을 때, 시작도시부터 끝도시까지 가는 최소비용을 구하는 문제입니다.
풀이
문제를 보자마자 최소거리를 구하는 알고리즘들을 떠올렸습니다. 코테에서 주로 나오는 그래프 알고리즘들은 아래와 같습니다. 이 문제에는 시작도시부터 끝까지의 거리를 구하는 문제이니 다익스트라(dijkstra)알고리즘을 사용하였습니다.
- 플로이드 와샬: 모든정점에서 모든정점 최단거리 https://blog.naver.com/ndb796/221234427842
- 크루스칼: MST(Minimum Spanning Tree 최소 신장 트리) 모든정점을 잇는 최소의 값 https://www.fun-coding.org/Chapter20-kruskal-live.html
- 다익스트라: 한 정점에서 모든 정점 최단거리: https://www.fun-coding.org/Chapter20-shortest-live.html
다익스트라를 간략하게 설명하자면, edge들을 비용 기준으로 입력받아
(heap queue이기 때문입니다. cost가 높은 불필요한 연산들을 줄여주는 효과가 있습니다.)
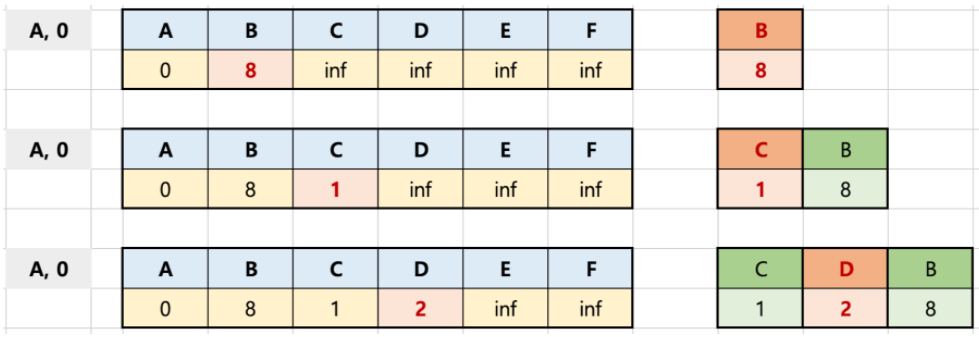
첫 정점에서 각 노드로 가는 거리와 현재 배열에 저장되어 있는 첫 정점에서 각 정점까지의 거리를 비교하는 것입니다.
코드
from sys import stdin
from heapq import heappush, heappop
from collections import defaultdict
stdin = open("input.txt", "r")
edges = defaultdict(lambda: [])
def dijkstra(start, end):
heap = []
heappush(heap, (0, start)) # 시작지점 힙에 추가
distance = [float('inf')] * (N + 1) # 각 정점사이의 거리 무한대로 초기화
distance[start] = 0 # 시작 지점 0으로 초기화
while heap:
cost, index = heappop(heap)
if(distance[index] < cost) : continue # 검사할 필요 없음
for e, c in edges[index]:
if distance[e] > cost + c:
distance[e] = cost + c
heappush(heap, (cost + c, e))
return distance[end]
# N 도시의 개수
# M 버스의 개수
N = int(stdin.readline())
M = int(stdin.readline())
# (출발 도시, 도착 도시, 버스 비용) M개
for _ in range(M):
start, end, cost = map(int, stdin.readline().split())
edges[start].append((end, cost))
# 시작지점, 끝 지점
start_city, end_city = map(int, stdin.readline().split())
print(dijkstra(start_city, end_city))이번 카카오 블채에서도 다익스트라 관련 문제가 나왔었습니다. 이 문제처럼 단순하게 시작지점과 끝지점이 아닌, 여러 경로의 최소거리를 구하는 문제였습니다. 플로이드 와샬로도 풀 수 있던 문제였습니다.
감사합니다~
다익스트라 코드 출처: https://jjangsungwon.tistory.com/28
'프로그래밍(Programming) > 알고리즘(Algorithm)' 카테고리의 다른 글
| 백준 - [Gold 4] 1922번 네트워크 연결 (0) | 2020.09.16 |
|---|---|
| 백준 - [Gold 2] 2533번 사회망 서비스(SNS) (2) | 2020.09.16 |
| 프로그래머스 월간 코드 챌린지 1 후기 (0) | 2020.09.11 |
| 백준 - [Gold 2] 2623번 음악프로그램 (0) | 2020.09.09 |
| 백준 - [Gold 5] 1759번 암호 만들기 (0) | 2020.09.09 |


